Head of Faculty
Mr S Marriott – smarriott@oriel.w-sussex.sch.uk
Deputy Head of Faculty
Mrs H Freeman – hfreeman@oriel.w-sussex.sch.uk
Assistant Head of Faculty
Mrs N Boys – nboys@oriel.w-sussex.sch.uk
Mr K Everington – keverington@oriel.w-sussex.sch.uk
Teaching Staff
Mrs C Carter- ccarter@oriel.w-sussex.sch.uk
Mr S Withell – swithell@oriel.w-sussex.sch.uk
Ms S Chowdhury – schowdhury@oriel.w-sussex.sch.uk
Mrs S Khan – skhan1@oriel.w-sussex.sch.uk
Mr S Anderson – sanderson@oriel.w-sussex.sch.uk
Miss K Catterick – kcatterick@oriel.w-sussex.sch.uk
Mr M Schmitz- mschmitz@oriel.w-sussex.sch.uk
Mr T Sandom – tsandom@oriel.w-sussex.sch.uk
Mr J Bywaters – jbywaters@oriel.w-sussex.sch.uk
Mr J Scott – jscott1@oriel.w-sussex.sch.uk
Mr M Pearce – mpearce@oriel.w-sussex.sch.uk
Mrs Y Zahid – yzahid@oriel.w-sussex.sch.uk
“Go down deep enough into anything and you will find mathematics.” – Dean Schlicter
The Mathematics department at Oriel aim to provide every student in our care with the opportunity to master the fundamentals of number in order that they become abstract thinkers and independent problem solvers. We work closely with other faculties in the school to ensure that skills, knowledge and vocabulary are widely transferable and consistent.
Our curriculum ensures that pupils master basic concepts thoroughly and then builds on these skills throughout the years so that they gain a cumulative knowledge. We spend longer on topics so that pupils become fluent in them.
We aim to instil confidence in students along with a growth mind-set that will help them overcome any anxiety about learning Mathematics.
Problem solving is integrated throughout every topic we study. Pupils of all standards are required to select, understand and apply the relevant mathematics principle. They represent concepts mathematical models, objects and pictures, and by making connections between different representations. This gives them the confidence, resilience and ability to tackle any problem rather than repeating routines without grasping the principles.
Lessons are not simply taught from textbooks, but utilise a wide ranging and varied set of classroom resources, intended to keep the subject interesting and engaging for all. These range from hands on worksheets and appropriate puzzle activities to eLearning resources, including MyMaths, Mathswatch, PinPoint Learning and a range of other platforms.
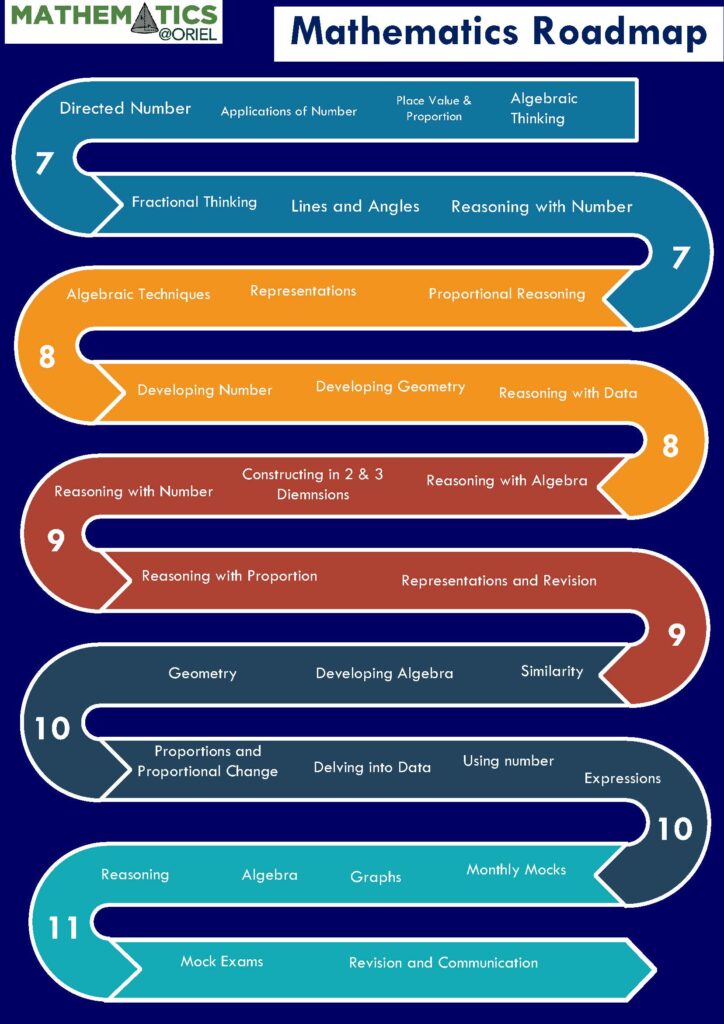
Year 7 & 8 Curriculum
In Year 7, students begin a programme of study tailored specifically to their attainment in year 6. The curriculum is designed along the principles of Mathematics mastery and allows students to study key concepts for extended periods of time so that they can become fluent in them and apply them in a range of contexts.
Students all have a fortnightly numeracy lesson where they work on exploring rich tasks or developing basic numeracy skills. These lessons are designed to complement learning across the curriculum.
We work closely with our locality schools to ensure a consistent approach to teaching key concepts as well as ensuring a deep collective understanding of the latest developments in the national curriculum.
A copy of the schemes of work can be found below:
GCSE Curriculum
In Year 9, 10 and 11 students are increasingly encouraged to develop good patterns of study and independent learning. Classroom work focuses on guiding students to reach their full potential in Mathematics, and we offer Edexcel entry-level examinations and Edexcel Linear GCSE (specification A 1MA1) at both Foundation and Higher levels. For that extra challenge for our more able students also study the Further Maths GCSE course.
The Schemes of Work for Year 9 and Year 10 can be found below:
Edexcel GCSE Specification A is a linear course. This means that all examinations are taken at the end of the course, namely in the summer of Year 11. The examination is split into 3 papers, and the first is a non-calculator examination.
The specification is here : Edexcel GCSE and GCE 2014 (pearson.com)
Calculators are allowed for the second and third paper. There are a number of calculators available. Two that have all the functions for examinations are:
CASIO FX-991EX Advanced Scientific Calculator

This is a calculator that students will need to study A-Level mathematics, so may be worth investing in for GCSE students hoping to carry on their studies.
Alternatively:
CASIO FX-83GTX Scientific Calculator

This is a more basic option, and therefore cheaper, but lacks functions needed for A-level study.
Both calculators will work perfectly for GCSE Mathematics, as will any other scientific calculator.
Post-16 Curriculum
In years 12 and 13 students have the opportunity to study Mathematics A2 Level and Further Mathematics AS and A2 level for the Edexcel Exam board.
The Mathematics course is made up of work across Pure Mathematics, Statistics and Mechanics. The program of study is fully proscribed by the exam board. Assessment is carried out using 3 papers. 2 Papers of Pure Mathematics and 1 paper covering Statistics and Mechanics. All 3 papers allow the use of a calculator.
The A Level Mathematics course is designed to allow students to explore the content and increasingly use the skills they have been learning to solve problems.
The Further Mathematics course is made of the 2 units of Core Pure Mathematics, 1 unit of Further Statistics and 1 unit of Further Mathematics. The course is delivered in such a way that students can undertake AS Level examinations at the end of Year 12.
In addition to the A Level course we also offer students the chance to study Core Mathematics with the AQA examination board. This qualification is suitable for students studying A Level courses requiring Mathematics who do not wish to study A Level maths. This is increasingly popular as an extra ½ option for students.
Regular homework and independent study is a key part of Post-16 and vital for success at the end of the courses.
Useful Study links
Every student will have been given a log in for the MyMaths website www.mymaths.co.uk
We have subscriptions with the following sites which have useful links and work sheets to help students with their maths
We also suggest that students use these links as well to further their understanding
Free Homework & Revision for A Level, GCSE, KS3 & KS2 (senecalearning.com)